Questions
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
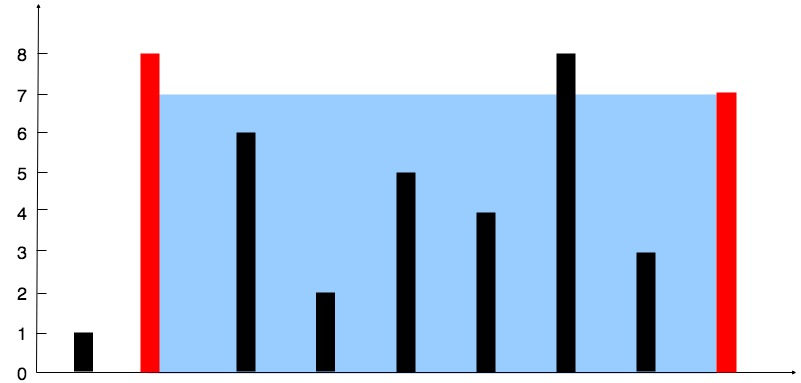
Example 1:
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49. Example 2:
Input: height = [1,1] Output: 1
Constraints:
n == height.length 2 <= n <= 105 0 <= height[i] <= 104
Solution
class Solution {
public:
int maxArea(vector<int>& height) {
int l(0), r(height.size()-1);
int max_vol(0);
while(l < r){
int min_h = min(height[l], height[r]);
int width = (r - l);
int volume = min_h * width;
max_vol = max(max_vol, volume);
if(height[l] < height[r]) l++;
else r--;
}
return max_vol;
}
};
This was the two pointer solution. The idea is to start with the widest container and move the pointer inward. Left pointer moves right if the left height is less than the right height, otherwise right pointer moves left. This is because the width is decreasing, so we need to find a taller container to increase the volume.
Keep comparing the volume with the max volume and update the max volume accordingly.